Binomial Theorem
(a+b)n = n∑(k=0) nCk a(n-k)) bk
Note I am using n∑(k=0) to mean the sum of the following formula for all values of k from o to n. Normally the upper value 'n' would be on the right of the sigma above the (k=0) but this is difficult to construct in web html. If you know how then please let me know.
Powers of (a+b)
Consider (a+b)n. The first five terms, including n=0, are (a + b)0 = 1 (a + b)1 = a + b (a + b)2 = (a + b)(a + b) = a2 + 2ab + b2 (a + b)3 = (a + b)(a + b)2 = (a + b)( a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3 (a + b)4 = (a + b)(a + b)3 = (a + b)( a3 + 3a2b + 3ab2 + b3) = a4 + 3a3b + 3a2b2 + ab3 + a3b + 3 2b2 + 3ab3 + b4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
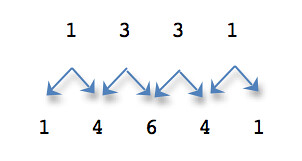
Pascal’s Triangle
The coefficients of the first four powers of (a + b) are
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Pascal showed that if you wrote the coefficients as shown above then the coefficients for next power can be determined by adding the adjacent coefficients of the previous line.
Permutation and Combination
It is necessary to discuss Permutation and Combination as the later is used in the Binomial Theorem.
Permutation
Consider how many patterns you can make from 3 characters “a b c”.
First choosing 2 characters, by inspection these are
ab, ac, ba, bc, ca, cb
i.e. a total of 6.
This quantity can be derived by following logic;
There are 3 ways to choose the first letter, and 2 ways remaining to choose the second, leaving the third as a given.
Therefore total number of ways is 3×2=6.
Note. The total number of patterns using all three characters is also 6, because after choosing 2 characters there is only one left, i.e. a choice of one.
abc, acb, bac, bca, cab, cba
and total number of ways is 3×2×1=6.
Consider how many patterns you can make from 4 characters “a b c d”.
First choosing 2 characters, by inspection these are:
ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc
i.e. a total of 12.
This quantity can be derived by following logic;
There are 4 ways to choose the first letter, and 3 ways remaining to choose the second, leaving the third as a given. Therefore total number of ways is 4×3=12.
Now choosing 3 characters, by inspection these are:
bac, bad, bca, bcd, bda, bdc,
cab, cad, cba, cbd, cda, cdb,
dab, dac, dba, dbc, dca, dcb,
i.e. a total of 24.
This quantity can be derived by following logic;
There are 4 ways to choose the first letter, and 3 ways remaining to choose the second, 2 ways choosing the third leaving the fourth as a given.as a given. Therefore total number of ways is 4×3×2=24.
Note. The total number of patterns using all three characters is also 24, because after choosing 3 characters there is only one left, i.e. a choice of one.
bacd, badc, bcad, bcda, bdac, bdca,
cabd, cadb, cbad, cbda, cdab, cdba,
dabc, dacb, dbac, dbca, dcab, dcba,
and total number of ways is 4×3×2×1=24.
General case, number of permutations for n items
If there are n different items, then the permutations (number of patterns) that can be made are:
n (n-1)(n-2)….(n-r+1)(n-r)(n-r-1) ….(4)(3)(2)(1)
where r is the general term. This number is known as n factorial and is written as n!
So 4! is 4×3×2×1.
Incidentally 0! = 1.
The only way I can explain this is to treat the choice of nothing is a valid choice, such as to choose no pudding at a meal is one possibility (weak I know but I will expand later).
The number of permutations of 3 items selected from n items is
n(n-1)(n-2) = [n(n-1)(n-2)(n-3)….(n-r+1)(n-r)(n-r-1)…(4)(3)(2)(1)]
----------------------------------------------------
(n-3)….(n-r+1)(n-r)(n-r-1)…(4)(3)(2)(1)
= n!
------
(n-3)!
The number of permutations of 3 items selected from n items is written as nP3 so
nP3 = n!
-----
(n-3)!
The number of permutations of r items selected from n items is written as nPr and by similar argument to above:
nPr = n!
-----
(n-r)!
Combinations
Combinations are similar to Permutations only the order of the selected items is of no importance, abc is treated the same as acb etc. In our example of choosing 3 characters from 4 we had 24 permutations, but 6 of theses were made up of the same 3 letters, abc, as were acd, abd and bcd. So the number of combinations of 3 characters from 4 is 4.
Similarly the number of combinations of two characters from 4 is ab, ac, ad, bc, bd, cd is 6.
The number of combinations of 4 characters from 4 is 1, remember the order of the items is not important.
The number of combinations of 3 characters from 4 is written as nC3.General term
Consider n items, what is the total number of combinations of r items from these n? This is written as nC3.It has been shown above that the number of permutations of r from n is:
But as the order of the r items is of no importance then every group of r different characters will give r! permutations that in combinations will be treated as the same. So nCr can be determined by calculating nPr and dividing by r!
nCr = n! / [(n-r)!)(r!)]
nCr = n! / [r!(n-r)!]
Specific examples.
1C1 = 1!/((1!)(0!)) = 1
2C0 = 2!/((0!)(2!)) = 1 2C1 = 2!/((1!)(1!)) = 2 2C2 = 2!/((2!)(0!)) = 1
3C0 = 3!/((0!)(3!)) = 1 3C1 = 3!/((1!)(2!)) = 3 3C2 = 3!/((2!)(1!)) = 3 3C3 = 3!/((3!)(0!)) = 3
4C0 = 4!/((0!)(4!)) = 1 4C1 = 4!/((1!)(3!)) = 4 4C2 = 4!/((2!)(2!)) = 6 ....
.... 4C3 = 4!/((3!)(1!)) = 4 4C4 = 4!/((4!)(0!)) = 1
These values are the same as the coefficients of the first four powers of (a + b) shown at start of article.
Note: the following relationships explain how the coefficients of (a+b)n increase to a maximum and then descend with the same values.
nCr = n!/(r!(n-r)!) = n!/((n-r)!r!) = nC(n-r) 10C3 = 10!/3!7! = (10×9×8)/(3×2×1) = 240 10C7 = 10!/7!3! = (10×9×8)/(3×2×1) = 240
Proving Binomial Theorem
(a+b)n = n∑(k=0) nCk a(n-k)) bk ............. (1)
Assume (1) is true
(a + b)(n+1) = (a + b)(a + b)n
= (a + b){ n∑(k=0) nCka(n-k) bk}
The general kth term for (a+b)n is n!/((n-k)!k!)
Consider the coefficient for a((n+1)-k)bk which are formed by
anCka(n-k)bk and bnC(k-1)a(n-(k-1))b(k-1)
It is the sum of the coefficients for a×a(n-k)bk and b×a(n+1-k)b(k-1)
a nCk+b nCk+1 = n!/((n-k)!k!) +n!/(n-(k-1))!(k-1)!)
= n!/((n-k)!(k-1)!){1/(k+1) + 1/(n+1-k)}
= n!/((n-k)!(k-1)!){(n+1-k+k)/((n+1-k)k)}
= n!/((n-k)!(k-1)!){(n+1)/((n+1-k)k)}
= ((n+1)!)/((n+1)-k)!k!)
NOTE: This is the same form as Binomial Theorem for (a+b)n+1
It has been shown that (1) is true for n = 0, 1, 2, 3, 4 and so all positive integers values of n are true by induction.
I believe my original handwritten notes are easier to understand than the above html so I have show this below.
Why is (0)! = 1
Briefly mentioned in main body above. Before considering factorial zero (0)! It is beneficial to consider three other forms of zero. I am not going back to basics in this section but just expanding the thoughts behind it.
Zero as a place holder
In our decimal system to write 2016, zero indicates there are no ‘100s’, otherwise it we could not distinguish it between 216. In early Babylonian time they had to use the context of the number to make this distinction and only towards the end of their era created a symbol.
Zero as nothing
A more abstract form. How many sweets in your pocket, 1, 2, many or none. Well I equate none with zero, but this was not formalised in the old western world until approx. 1250, from India via Moors in Spain. (See New World Encyclopedia http://www.newworldencyclopedia.org/entry/0_(number).
Defining zero
1 + 0 = 1, 1 – 0 = 1, 1 x 0 = 1, 1 / 0 indeterminate or more generally a + 0 = 1, a – 0 = 1, a x 0 = 1, a / 0 indeterminate
Note division by zero is not supported in our use of zero. I assume it is because all values of subtracting 0 are possible.
Today we all except 0 zero readily without having to question it’s meaning, and find it hard to understand why the ancients found it so difficult a concept.
Power such as (a)0
Now we write a×a×a as a3 and a×a×a×a×a as a5.
We note (a×a×a)×(a×a×a×a×a) = (a×a×a×a×a×a×a×a) which is the same as a5. This is the same as a3×a5 = a8.
Similarly (a×a×a×a×a)/(a×a×a) = (a×a) which is the same as a2 and (a×a×a)/(a×a×a×a×a) = 1/(a×a) which is the same as 1/a2 which we write as a-2. This is the same as a5/a3 = a2 and a3/a5 = a-2.
So we see that in general terms ai×aj = ai+j and ai/aj = ai-j. However in the division it is possible to have aj/aj = aj-j = a0, but we know that one value divided by the same value is equal to 1, so aj/aj = aj-j = a0 = 1
.(0)! - Factorial 0
I wrote the above to show how we in time accept constructions and they become the norm, for example when we do the following 27÷4 and mentally say this 63/4 forgetting that it the number of times we can subtract 4 from 27 and how many remain.
In the short term of trying to find a better explanation of why (0)! = 1 on the web but with little success. It has been shown that nCr = n!/(n-r)!r! but consider r=n so nCn = n!/(n-n)!n! = n!/(0)!n!= 1/(0)!
But nCn = 1 as there is only one way you can create a group using all of a sets members when order is not important. Therefore for consistency (0)! = 1.
Thinking about Combinations and not just processing the formula, recall that (n-r)! in the denominator is determined by the number of items not chosen and is what is left after the r components have been selected. The r! in the denominator is there to remove the number of permutations as we are only concerned with the group not the order. Therefore by selecting all n there are no items left over, hence the (0)!, and I consider there is only one way to create a group using all items, there is also only 1 way to select a group using none of the items. A zero set is still a set.
None integer values for n
What about when a and/or b are not integers,
let i/j be a and p/q be b where i,j,p,q are all positive integer then we are investigating
(i/j+p/q)n = {(iq+pj)/(jq)}n = (iq+pj)n/(jq)n
The numerator is of the form (a+b)n and the denominator is just an integer raised to the power of n.
Of course decimal values can be written as fractions and treated as above.
Negative integer values for n
This is quite easy, as (a+b)-n = 1/{(a+b)n} then it is just the reciprocal of the positive n.
a >> b
I graduated in Physics, many years ago now, but I remember using the binomial theorem approximation many times when a>>b.
First a numeric example where a=100, b=0.001 and n=3
(100 + 0.01)3 = 1003 + 3x1002x0.01 + 3x100 x0.012 + 0.013
= 1,000,000 + 300 + 0.03 + .000001
= 1,000,300.030001
≈ 1,000,300
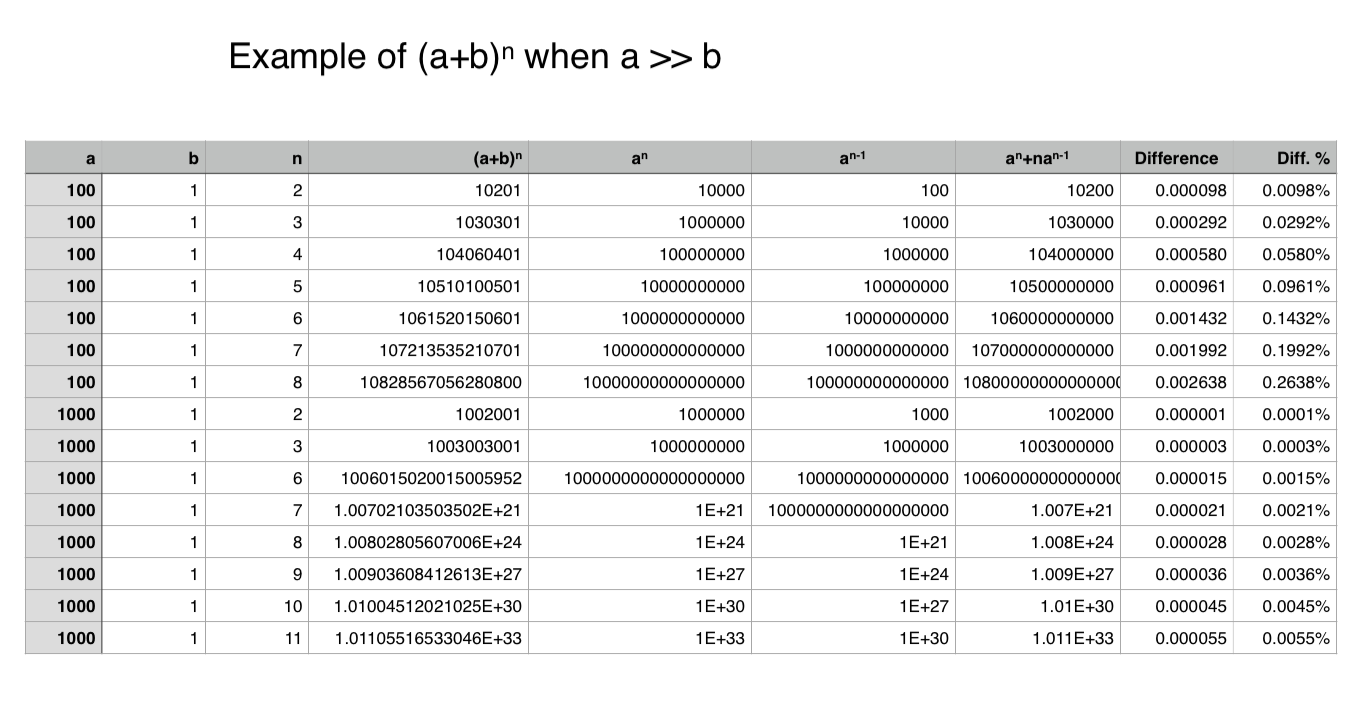
(a + b)3 ≈ a3 + 3a 2b when a >> b
Similarly (100 +0.01)2 = 1000 + 2 + 0.0001 ≈ 1002
In General
(a + b)n ≈ an + nanb when a >> b
The following image is from a spread sheet I built to investigate the above findings for a >> b.