Euclid Prop. 1
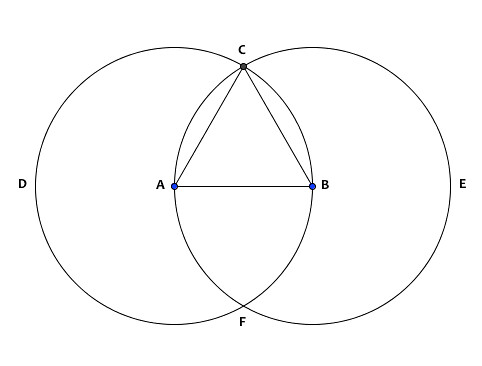
On a given finite right line (AB) to construct an equilateral triangle.
Sol.—With A as centre, and AB as radius, describe the circle BCD (Post. iii.).
With B as centre, and BA as radius, describe the circle ACE, cutting the former circle in C. Join CA, CB (Post. i.).
Then ABC is the equilateral triangle required.
Because A is the centre of the circle BCD, AC is equal to AB. Again, because B is the centre of the circle ACE, BC is equal to BA. Hence we have proved AC = AB, and BC = AB. Therefore AC is equal to BC; therefore the three lines AB, BC, CA are equal to one another. Hence the triangle ABC is equilateral; and it is described on the given line AB.
Exercises.
The following exercises are to be solved when the pupil has mastered the First Book:--
Rhombus
Casey's lozenge is what I call a rhombus. The following is from Wikipedia.
Traditionally, in two-dimensional geometry, a rhomboid is a parallelogram in which adjacent sides are of unequal lengths and angles are oblique.
A parallelogram with sides of equal length (equilateral) is a rhombus but not a rhomboid.
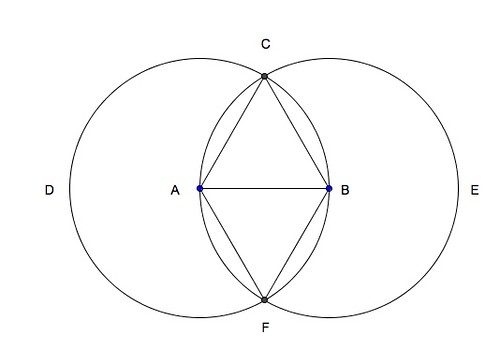
1. If the lines AF, BF be joined, the figure ACBF is a lozenge.
It can be shown that triangle ABF is equilateral by using above method.
As both triangles have common side AB, then all sides are equal, i.e.
AC = CB = BF = FA and ∠CAB = ∠FBA = 60∘ ∴ AF || BC (alt. ang.s equal) Draw CF and a similar argument will show AC || FB ∴ ABCD is a rhombus (lozenge) (opp. sides equal and parallel)
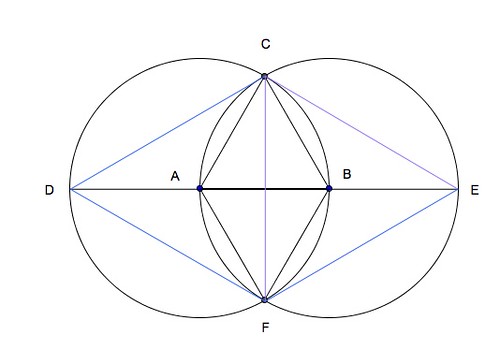
2. If AB be produced to D and E, the triangles CDF and CEF are equilateral.
∠ADC = ∠ACD (∆ADC isos. AD=DC)
∠BAC = ∠ADC +∠ACD (External ang. of tri. ADC)
= 60∘ (proven above)
∴ ∠ADC = ∠ACD =30∘
∠CAB = ∠FAB = 60∘ (∆ACB & ∆FAB both equilateral)
∴ ∠CAF = 120∘
∠ACF + ∠AFC = 60∘ (angles of triangle = 180∘)
∠ACF = ∠AFC = 30∘ (isos. ∆ACF AC = AF)
∴ ∠DCF = ∠DFC = 60∘
∴ ∠CDF = 60∘ (angles of triangle = 180∘)
∴ ∆CDF is equilateral (All 3 angles = 60∘)
By similar argument it can be shown that ∆CFE is also equilateral
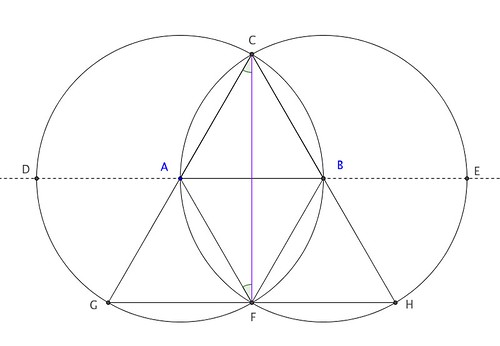
3. If CA, CB be produced to meet the circles again in G and H, the points G, F, H are collinear, and the triangle GCH is equilateral.
∠CAB = ∠BAC = 60∘ (proven above) ∴ ∠GAF = 60∘ (CAG is str. line = 180∘) ∠AGF = ∠CAB = 60∘ (corr. ang.s CB || AF) ∴ ∠AFG = 60∘ (angles of triangle = 180∘) ∴ ∆AGF is equilateral (all ang.s = 60∘) Similarly ∆BFG is equilateral ∴ ∠BHF = 60∘ ∠AFB = 60∘ (proven previously) ∴ GFH is str. line (∠GFA + ∠AFB + ∠BFH = 180∘) and ∆CGH is equilateral (all 3 ang.s = 60∘)
4. If CF be joined, CF² = 3AB².
CG² = GF² + CF² ∴CF² = CG² - GF² = CG² - AB² But CG² = 2AC² = 2AB² and CG² = 4AB² ∴ CF² = 4AB² - AB² = 3AB²
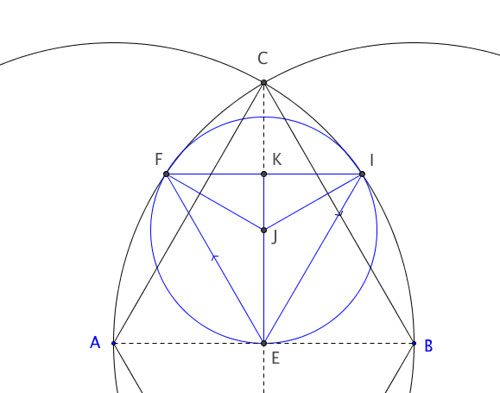
5. Describe a circle in the space ACB, bounded by the line AB and the two circles.
Draw EF parallel to BC
Draw EI such that EI=EF and I lies on circle centred on A
Join FI
∠EFI = ∠EIF (∆EFI isos.)
Draw KE perpendicular to FI, K lying on FI
∠FEK = 180∘ - ∠EKF - ∠EFI
= 180∘ - 90∘ - ∠EFI
= 90∘ - ∠EFI
= 90∘ - ∠EIF
= ∠IEK
∴ ∆FKE ≣ ∆IKE (2 angles & included side =)
∴ FK = IK
∴ K lies on CD (angle bisector equi-distant from sides)
∠FKE = 90∘
= ∠BEK (Proven previously)
∴ FI || AB (Alternate angles =)
∠AEF = ∠EBF ( EF parallel to BC)
= 60∘ ( Constructed previously)
= ∠EFI ( alt. ang.s FI || AB)
= ∠EIF ( proven)
= ∠FEI (ang.s tri. = 180∘)
∴ ∆EFI is equilateral (all 3 ang.s = 60∘)
Draw angle bisectors for ∠EFI & ∠EIF intercepting at point J
J is centre of circle passing through E, F and I.
(ang. bisectors of equil. tri. equi. dist from vertices)
∴ J is centre of required circle