Straight Line
Join two points A,B by constructing a straight line that they both lie upon terminating at their respective locations.
Straight line constructed by positioning straight edge touching both locations.
Straight line constructed by positioning straight edge touching both locations.
Angles
|
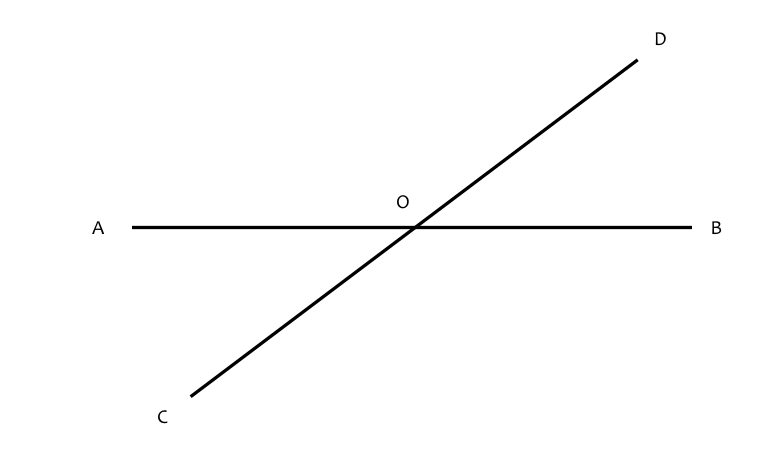
Consider 2 straight lines AB, CD intersecting at O
AO can be rotated about O so that it lies upon CO, occupying the same set of points The amount of revolution is known as the angle AOC If AO continues to rotate about O until it once again overlays its original position it will have performed 1 revolution. One measure divides 1 revolution into 360 degrees, each degree into 60 minutes and each minute into 6o seconds i.e. 1 revolution = 360 degrees = 2,160 minutes = 1,296,000 seconds (5º is shorthand way of writing 5 degrees) |
Right Angles
|
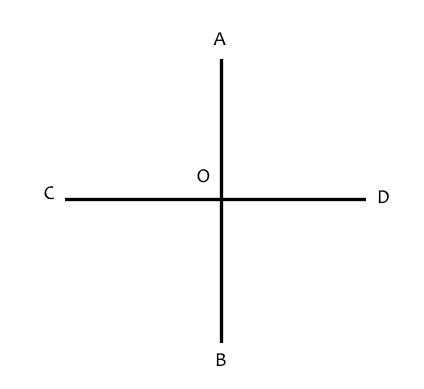
CD is a straight line.
O is a position that lies on CD and AO is another straight line. ∠AOD is the amount a line OD needs to be rotated to position it over OA. (“∠” is the symbol for angle) All values for this angle are possible, including the one that satisfies ∠AOD = ∠AOC This angle is called a right angle (rt. ang.) and AD is said to be perpendicular to CD If one rotates AO another 1 rt. ang. anti-clockwise it lies on CO since ∠AOD = ∠AOC = 1 rt. ang This is equivalent to rotating OD through 2 rt. ang.s. But CO is part of straight line CD, so a straight line may be thought of the addition of 2 rt. ang.s. BO is drawn such that ∠COB = ∠BOD then as before these are rt. ang.s then as AB is also built of 2 rt. angs. it is also a straight line. So 4 rt. ang.s = 1 revolution = 360º ∴ 1 rt. ang. = 90º (Currently we have shown how a rt. ang. can exist, later it will be shown how to construct one) |
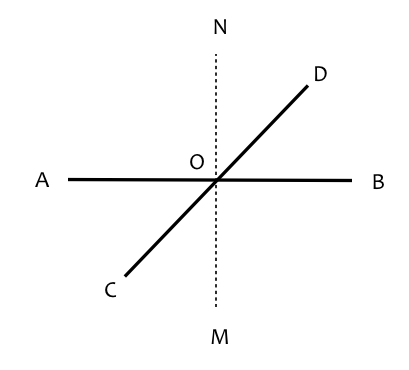
Opposite angles of intersecting lines are equalAB & CD are two straight lines intersecting at O. Let MN be a line passing through O perpendicular to AB ∴ ∠MOB = ∠NOB = ∠AON = ∠AOM = 1 rt. ang. ∠DOB = 1 rt. ang. - ∠NOD ∠AOC = 2 rt. ang.s - ∠AOD = 2 rt. ang.s - 1 rt. ang. - ∠NOD = 1 rt. ang. - ∠NOD = ∠DOB Similalry ∠DOA = ∠COB AB & CD are two straight lines intersecting at O. Let MN be a line passing through O perpendicular to AB ∴ ∠MOB = ∠NOB = ∠AON = ∠AOM = 1 rt. ang. ∠DOB = 1 rt. ang. - ∠NOD ∠AOC = 2 rt. ang.s - ∠AOD = 2 rt. ang.s - 1 rt. ang. - ∠NOD = 1 rt. ang. - ∠NOD = ∠DOB Similalry ∠DOA = ∠COB |